一、数据结构基本概念

1. 基本概念和术语

  • 数据

数据是信息的载体，是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序所识别和处理的符号的集合。

  • 数据元素

数据元素是数据的基本单位。

  • 数据对象

数据对象是具有相同性质的数据元素的集合。

  • 数据类型

数据类型是一个值的集合和定义在此集合上的一组操作的总称。

  • 数据结构

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。

2. 数据结构三要素

  • 数据的逻辑结构

逻辑结构是指数据元素之间的逻辑关系。

逻辑结构

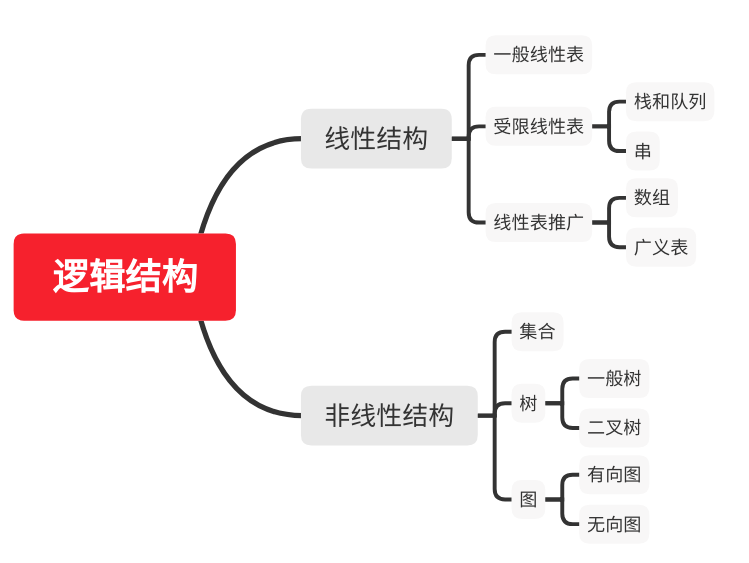
  • 数据的存储结构

存储结构是指数据在计算机中的表示，也称之为物理结构，主要有以下几种方式：

  1. 顺序存储
  2. 链式存储
  3. 索引存储
  4. 散列存储（哈希存储）
  • 数据的运算

二、算法和算法评价

1. 算法的基本概念和特性

  • 算法概念

算法是对特定问题求解步骤的一种描述，举个简单的例子，如何把一头大象放进冰箱的解答就是一个算法。

  • 算法特性

    • 有穷性

    • 确定性

    • 可行性

    • 输入

    • 输出

2. 算法的评价度量

  • 时间复杂度

算法中所有语句的频度之和为T(n)，时间复杂度主要分析T(n)的数量级。

$$ T(n) = O(f(n)) $$
  • 空间复杂度

算法的空间复杂度S(n)定义为算法所耗费的存储空间，它是问题规模n的函数。

$$ S(n) = O(g(n)) $$

三、牛刀小试

  1. 已知一个算法由下列递归方程表示，求该算法的时间复杂度。
$$ T(n) \begin{cases} 1,&n = 1\\ 2T(n/2) + n,&n > 1 \end{cases} $$

解：设\(n = 2^k (k>=0)\)，根据题目有：

\(T(2^k) = 2T(2^{k-1}) + 2^k = 2^2T(2^{k-2}) + 2^22^k\)，

\(\therefore\)得出一般递推式：

\(T(2^k) = 2^kT(2^0) + k2^k = (k + 1)2^k\)，即：

\(T(n) = 2^{log_2n} + log_2n*n = n(log_2n + 1)\)

\(\therefore O(n) = nlog_2n\)

  1. 计算下列程序段的时间复杂度
1
2
3
4
5
i = 1; k = 0;
while(i < n - 1){
    k = k + 10 * i;
    i++;
}

\(O(n) = n\)

1
2
3
4
y = 0;
while((y + 1) * (y +1) <= n){
    y = y + 1;
}

\(O(n) = \sqrt n\)