前言

在面试中，面试官很容易问到B树这种数据结构，要去熟练的掌握这个数据结构还是有一定的难度，为了提升自身的技术深度，我特地花了一定的时间梳理和总结一下B树的全部概念与操作。

B树的概念

B树是一种多路平衡查找树，不同于二叉平衡树，他不只是有两个分支，而是有多个分支，一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树，B树用于磁盘寻址，它是一种高效的查找算法。

B树的性质

  1. 根节点至少有2个子女
  2. 每个非根节点所包含的关键字个数x满足以下关系：⌈m/2⌉−1⩽x⩽m−1\lceil m/2 \rceil - 1 \leqslant x \leqslant m - 1
  3. 所有叶子结点都在同一层
  4. 除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：⌈m/2⌉⩽k⩽m\lceil m/2 \rceil \leqslant k \leqslant m

B树数据结构描述

一个B树结点包含了以下关键信息：

  • 关键字数量
  • 关键字数组指针
  • 孩子数组指针
  • 父亲结点指针

为了写代码方便一点，还需要包含以下信息：

  • 树的阶数
  • 孩子数量

用代码表示如下：

1
2
3
4
5
6
7
8
typedef struct Node {
    int level; // 树的阶数
    int keyNum; // 关键字数量
    int childNum; // 孩子数量
    int* keys; // 关键字数组
    struct Node* parent; // 父亲指针
    struct Node** children; // 孩子指针数组
} Node;

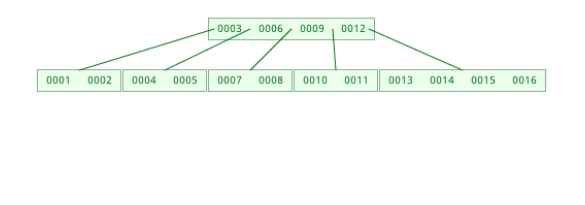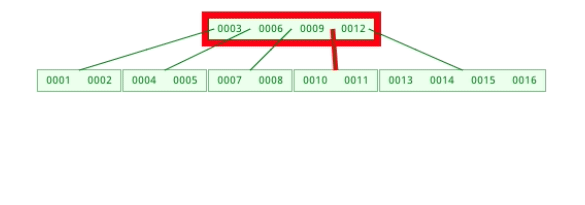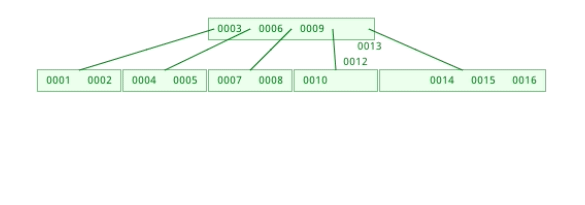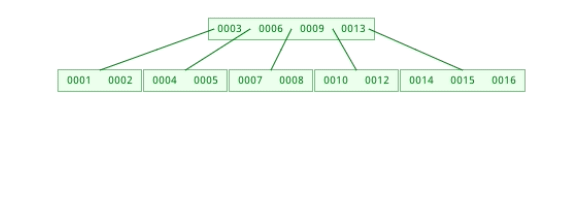
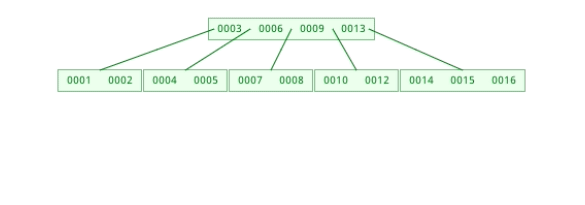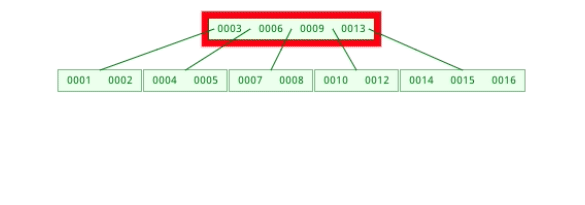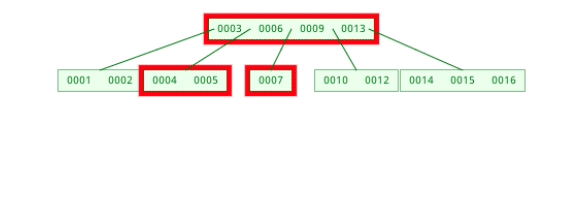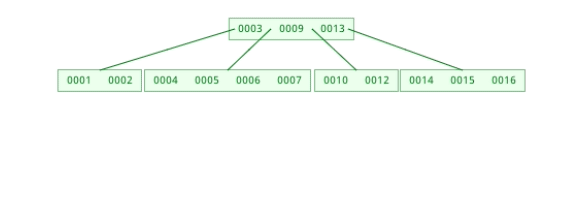
image

B树的插入

B树的插入操作只能在叶子结点上进行操作，而且叶子结点上关键字的个数要严格满足B树的性质：⌈m/2⌉−1⩽x⩽m−1\lceil m/2 \rceil - 1 \leqslant x \leqslant m - 1

插入步骤如下：

  1. 寻找合适的叶子结点
  2. 在叶子结点上找到合适的插入位置
  3. 插入后判断关键字个数是否超过m-1，如果超过则结点需要分裂，分裂从中间劈开，并将中间的元素插入到当前结点的父亲结点中，判断父亲结点关键字个数是否超过m-1，如果超过继续分裂，重复第3步

用1，2，3，4，5这个序列组建一棵5阶B树举例：

image

B树的删除

B树的删除操作较为复杂，需要分情况讨论：

要删除的结点在非叶子结点上：

从当前关键字左边的子树中找到叶子上最大的关键字，将待删除的关键字和这个关键字进行对调，将非叶子结点的删除转化为叶子结点的删除

image

要删除的结点在叶子结点上：

情况1：当前叶子结点的关键字个数x>⌈m/2⌉−1x > \lceil m/2 \rceil - 1，此时可以直接删除，如下图中我想要删除18，那么就要执行以下操作：

image

情况2：当前叶子结点的关键字个数x=⌈m/2⌉−1x = \lceil m/2 \rceil - 1，此时删除之后叶子结点不满足关键字最小个数，那么第一步先去跟父亲借一个结点补过来，同时父亲从它兄弟借一个补上来；如果借完之后兄弟结点的关键字个数x<⌈m/2⌉−1x < \lceil m/2 \rceil - 1，借这条路就走不通了，则需要进行合并操作，将当前叶子结点和它的兄弟以及父亲中兄弟俩夹住的那个关键字合并成一个结点

  • 可以借，删除11，具体删除情况如下：

image

  • 不可以借，需要合并，删除8，具体删除情况如下：

image

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int level; // 树的阶数
    int keyNum; // 关键字数量
    int childNum;
    int* keys; // 关键字数组
    struct Node* parent; // 父亲指针
    struct Node** children; // 孩子指针数组
} Node;

// 初始化结点
Node* initNode(int level) {
    Node* node = (Node*)malloc(sizeof(Node));
    node -> level = level;
    node -> keyNum = 0;
    node -> childNum = 0;
    node -> parent = NULL;
    node -> keys = (int*)malloc(sizeof(int) * (level + 1));
    node -> children = (Node**)malloc(sizeof(Node*) * level);
    for (int i = 0; i < level; i++) {
        node -> keys[i] = 0;
        node -> children[i] = NULL;
    }
    return node;
}

// 从结点中找到合适的插入位置
int findSuiteIndex(Node* node, int data) {
    int index;
    for (index = 1; index <= node -> keyNum; index++) {
         if (data < node -> keys[index])
             break;
    }
    return index;
}

// 往结点中插入数据
void addData(Node* node, int data, Node** T) {
    int index = findSuiteIndex(node, data);
    for (int i = node -> keyNum; i >= index; i--) {
        node -> keys[i + 1] = node -> keys[i]; 
    }
    node -> keys[index] = data;
    node -> keyNum = node -> keyNum + 1;
    if (node -> keyNum == node -> level) {
        // 开始分裂，找到中间位置
        int mid = node -> level / 2 + node -> level % 2;
        // 初始化左孩子节点
        Node* lchild = initNode(node -> level);
        // 初始化有孩子节点
        Node* rchild = initNode(node -> level);
        // 将mid左边的值赋值给左孩子
        for (int i = 1; i < mid; i++) {
            addData(lchild, node -> keys[i], T);
        }
        // 将mid右边的值赋值给右孩子
        for (int i = mid + 1; i <= node -> keyNum; i++) {
            addData(rchild, node -> keys[i], T);
        }
        // 将原先节点mid左边的孩子赋值给分裂出来的左孩子
        for (int i = 0; i < mid; i++) {
            lchild -> children[i] = node -> children[i];
            if (node -> children[i] != NULL) {
                node -> children[i] -> parent = lchild;
                lchild -> childNum ++;
            }
        }
        // 将原先节点mid右边的孩子赋值给分裂出来的右孩子
        int index = 0;
        for (int i = mid; i < node -> childNum; i++) {
            rchild -> children[index++] = node -> children[i];
            if (node -> children[i] != NULL) {
                node -> children[i] -> parent = rchild;
                rchild -> childNum ++;
            }
        }
        //判断当前节点是不是根节点
        if (node -> parent == NULL) {
            // 是根节点
            Node* newParent = initNode(node -> level);
            addData(newParent, node -> keys[mid], T);
            newParent -> children[0] = lchild;
            newParent -> children[1] = rchild;
            newParent -> childNum = 2;
            lchild -> parent = newParent;
            rchild -> parent = newParent;
            *T = newParent;
        }
        else {
            // 不是根节点
            int index = findSuiteIndex(node -> parent, node -> keys[mid]);
            lchild -> parent = node -> parent;
            rchild -> parent = node -> parent;
            node -> parent -> children[index - 1] = lchild;
            if (node -> parent -> children[index] != NULL) {
                for (int i = node -> parent -> childNum - 1; i >= index; i--) {
                    node -> parent -> children[i + 1] = node -> parent -> children[i];
                }
            }
            node -> parent -> children[index] = rchild;
            node -> parent -> childNum ++;
            addData(node -> parent, node -> keys[mid], T);
        }
    }
}

Node* findSuiteLeafNode(Node* T, int data) {
    if (T -> childNum == 0)
        return T;
    else {
        int index = findSuiteIndex(T, data);
        return findSuiteLeafNode(T -> children[index - 1], data);
    }
}

Node* find(Node* node, int data) {
    if (node == NULL) {
        return NULL;
    }
    for (int i = 1; i <= node -> keyNum; i++) {
        if (data == node -> keys[i]) {
            return node;
        }
        else if (data < node -> keys[i]) {
            return find(node -> children[i - 1], data);
        }
        else {
            if (i != node -> keyNum && data < node -> keys[i + 1]) 
                return find(node -> children[i], data);
        }
    }
    return find(node -> children[node -> keyNum], data);
}

// 插入结点
void insert(Node** T, int data) {
    Node* node = findSuiteLeafNode(*T, data);
    addData(node, data, T);
}

void printTree(Node* T) {
    if (T != NULL) {
        for (int i  = 1; i <= T -> keyNum; i++) {
            printf("%d ", T -> keys[i]);
        }
        printf("\n");
        for (int i = 0; i < T -> childNum; i++) {
            printTree(T -> children[i]);
        }
    }
} 

int main() {
    Node* T = initNode(5);
    insert(&T, 1);
    insert(&T, 2);
    insert(&T, 6);
    insert(&T, 7);
    insert(&T, 11);
    insert(&T, 4);
    insert(&T, 8);
    insert(&T, 13);
    insert(&T, 10);
    insert(&T, 5);
    insert(&T, 17);
    insert(&T, 9);
    insert(&T, 16);
    insert(&T, 20);
    insert(&T, 3);
    insert(&T, 12);
    insert(&T, 14);
    insert(&T, 18);
    insert(&T, 19);
    insert(&T, 15);
    printTree(T);
    Node* node = find(T, 7);
    if (node) {
        for (int i = 1; i <= node -> keyNum; i++) {
            printf("%d ", node -> keys[i]);
        }
        printf("\n");
    }
    return 0;
}